题目背景

现在正处于疫情防控的关键时期，大家要经常洗手，防止接触感染。

题目描述

给定一张含有n 个点的无向完全图，其中m 条边是白边，其余是黑边。

现在需要你求出同色的三元环（或者说，三角形）的个数。

输入格式

第一行整数n,m，意义如题。

剩下的m 行每行两个整数u,v，代表白边的两个端点。保证给出的白边没有重边和自环。

输出格式

一行一个整数，为答案。

输入输出样例 #1

输入 #1

5 3
1 5
2 5
3 5

输出 #1

4

说明/提示

• 对于20\% 的数据，满足n \leq 200；

• 对于50\% 的数据，满足n \leq 2000；

• 对于100\% 的数据，满足1 \leq n \leq 10^5,1 \leq m \leq 3\times 10^5。

思路

不考虑有黑白边，求n个点的完全图能画多少个三角形。

三角形中的一个点连着三角形的两条边，所以图上每个点中，枚举两条边后加上外面一条边后就是一个三角形（好像说了很多重要但是很绕的废话...），因为是完全图，所以只要考虑一个点的两条边，外面的第三条边一定存在。排列组合，有n个点，一个点上有n-1条边，选出第一条边后还剩n-2条边选第二条边。这时候考虑去重，第一条边和第二条边先后取是同一个三角形重复计数两次，三角形有三个点会重复计数三次，整理答案为\frac{n(n-1)(n-2)}{6}，而且一定能除尽。

加入黑白边规则，我们只要在原本的三角形个数里减去有杂色边的三角形就行了，有杂色的三角形肯定是两条同色边+一条异色边，那么这个三角形的其中两个端点肯定是连着一条黑边和一条白边，枚举这种点边的组合的话只要统计这个点上有多少条白边，其余都是黑边，白边乘黑边即可mp_i*(n-mp_i-1)（mp_i为i点白边个数），然后因为每个杂色三角形都有两个这样的点，所以除以二去重。

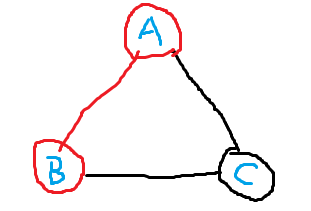
如图，杂色三角形一定包含A点和B点两个杂色边

代码

#include <bits/stdc++.h>
#define int long long//细节long long
using namespace std;
int n,p,ans,mp[114514];
signed main()
{
	cin>>n>>p;
	int x,y;
	ans=n*(n-1)*(n-2)/3;//这里除以3
	for(int i=1;i<=p;i++) {
		cin>>x>>y;
		mp[x]++;//边都不用存直接存数量
		mp[y]++;
	}
	for(int i=1;i<=n;i++)
		ans-=mp[i]*(n-mp[i]-1);
	ans=ans/2;//这里除以2相当于一块去重了，问就是懒
	cout<<ans;
	return 0;
}